数据结构

2019-08-24

数据结构还是比较重要的，是优化技巧中的必备技能。曾经有段时间很认真的读了严蔚敏那本书，后来竟然全都还回去了，应试学习价值确实不大。最近有时间整理一下，下次回顾时方便点。

栈

栈是一种线性数据结构，只能从栈顶添加和取出元素。

基本原则：先进后出（LIFO, Last In First Out）。

常见使用场景：

Undo 操作
系统调用栈

栈的基本设计：

public interface Stack<E> {
// 时间复杂度 均为 O(1 )
    int getSize();
    boolean isEmpty();
    void push(E e); // 压栈/入栈
    E pop(); // 取出并删除栈顶元素
    E peek(); // 取出栈顶元素
}

队列

队列是一种线性数据结构，从队尾添加元素，从队首取出元素。

基本原则：先进先出（FIFO, First In First Out）。

队列的基本设计：

public interface Queue<E> {
    int getSize();
    boolean isEmpty();
    void enqueue(E e);  // 入队
    E dequeue();  // 出队
    E getFront(); // 取出队首
}

复杂度均为 $O_{(1)}$，在底层为数组实现的 Queue 中，出队操作复杂度为$O_{(1)}$。（每次出队，删除array[0]，其他元素向前移动）

循环队列

每次删除或者添加时，移动头尾指针。

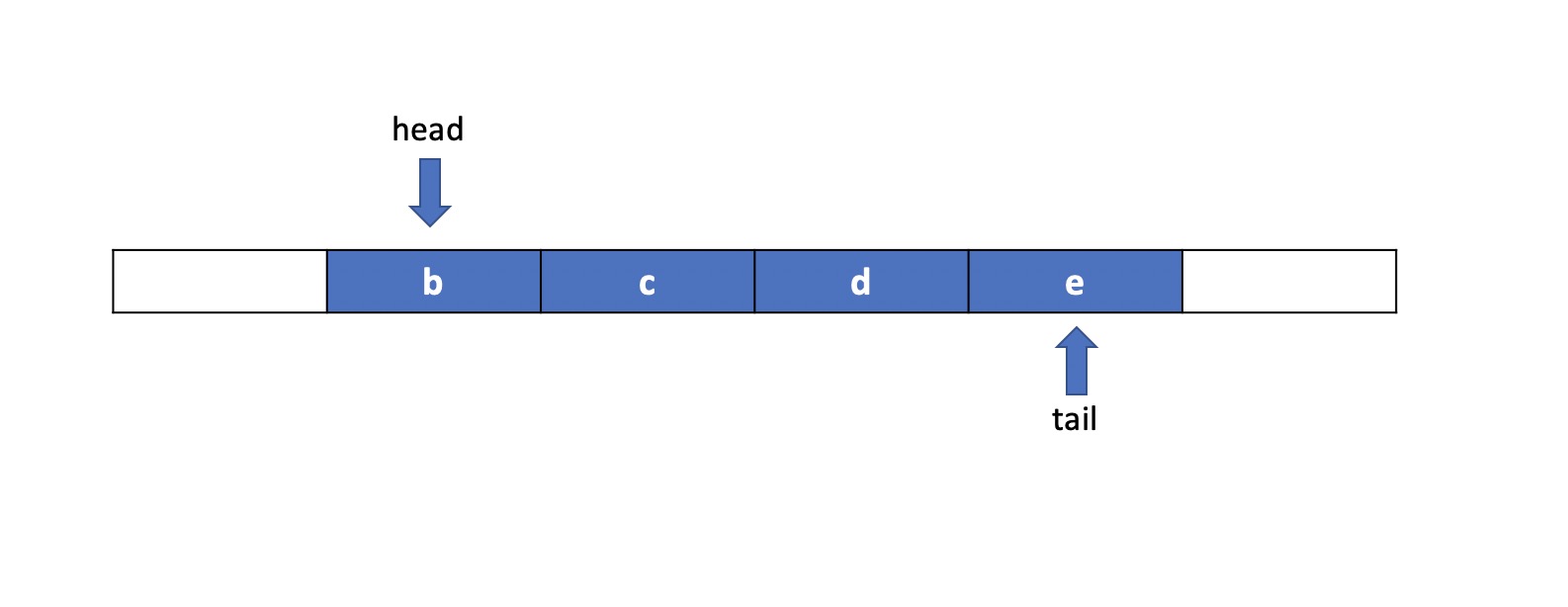
到头之后的操作：

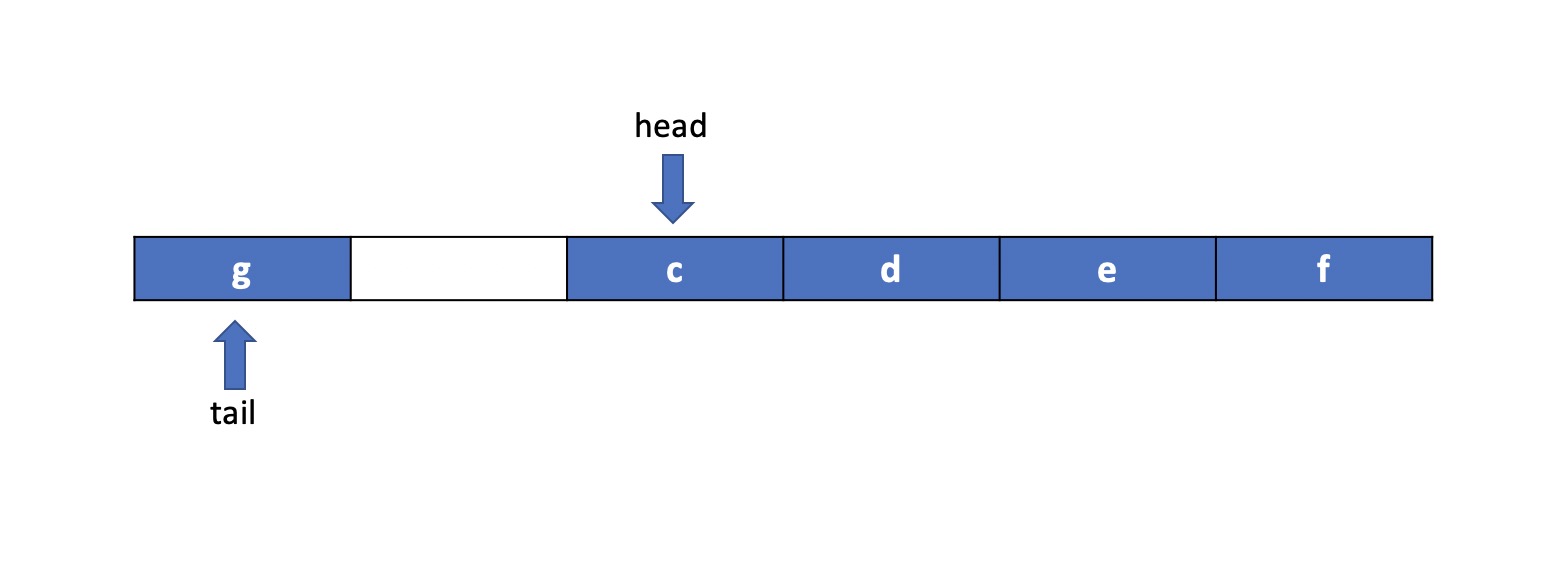
这样队列的为空和需要扩容判断条件就是：

head == tail 队列为空

(tail + 1) % capacity == head 队列满

这样队列的入队均摊时间复杂度就是 $O_{(1)}$了。（只需移动指针）

链表

动态数组、栈、队列，底层依托静态数组，靠resize解决固定容量问题。而链表则是真正的动态数据结构。

数组、栈、队列和链表的对比：

数组：支持索引快速查询，索引有语意时比较高效。
栈：先进后出特性。
队列：先进先出特性。
链表：优点在于动态，但不支持索引查询。

链表的具体操作：

在链表头添加元素：

node.next = head
head = node

为某个位置添加元素。

先找到前一个位置的元素 prev 。
node.next = prev.next
prev.next = node

删除某个位置的元素：

先找到前一个位置的元素 prev 。
delNode = prev.next
prev.next = delNode.next
delNode.next = null

可以设置虚拟头节点，帮助链表更好的添加元素。

链表的时间复杂度：

添加操作 $O_{(1)}$
- addLast(e) $O_{(1)}$
- addFirst(e) $O_{(1)}$
- add(index, e) $O_{(n/2)}$ = $O_{(n)}$
删除操作 $O_{(n)}$
- removeLast(e) $O_{(1)}$
- removeFirst(e) $O_{(1)}$
- remove(index, e) $O_{(n/2)}$ = $O_{(n)}$
修改操作 $O_{(n)}$
- set(index, e) $O_{(n)}$
查找操作 $O_{(n)}$
- get(index) $O_{(n)}$
- contains(e) $O_{(n)}$

扩展：了解双链表（带前后指针），循环双链表（最后一个指向虚拟头节点），同时可以使用链表来实现栈和队列。

树结构

二分搜索树

二分搜索树的每个节点的值：

大于其左子树的所有节点的值
小于其右子树所有节点的值
每棵子树都是一个二分搜索树
存储的元素具有可比较性
一般情况下节点值并不重复，如果重复需更改条件1 或条件2 变为大于等于或小于等于

二分搜索树的添加：

递归比较
大于当前节点递归访问右子树并判断
小于当前节点低轨访问右子树并判断
直到当前访问子树为空，并且大于或小于当前子树父节点，进行插入操作

二分搜索树的深度优先遍历：

可以更快的找到问题的解，常用与算法设计中，如最短路径。

前序遍历

1
2
3

visit(node)
visit_recursion(node.left)
visit_recursion(node.right)

中序遍历

1
2
3

visit_recursion(node.left)
visit(node)
visit_recursion(node.right)

后序遍历

1
2
3

visit_recursion(node.left)
visit_recursion(node.right)
visit(node)

例如：

      28
     / \
   /     \
  16     30
 / \     / \
13  22  29 42

前序遍历：28, 16, 13, 22, 30, 29, 42

中序遍历（注意中序遍历结果是有序的）：13, 16, 22, 28, 29, 30, 42

后序遍历：13, 22, 16, 29, 42, 30, 28

二分搜索树非递归写法，需要借助栈。比如前序遍历：先将要根节点压入栈，访问栈顶的根节点，然后将右子树（注意先右子树）、左子树，然后访问栈顶元素，再将栈顶元素的右子树、左子树压入栈…… 直到栈为空。

二分搜索树的层次遍历

可以借助队列来实现。首先让根节点入队，然后访问队首元素，将其左子树、右子树（注意顺序）从队尾入队…… 直到队空。

二分搜索树删除节点

删除最大最小值：

如果是叶子节点，可以直接删除
如果是非叶子结点，那一定是一个单枝的节点（只拥有左子树或右子树），将自己的孩子节点替换掉要删除的节点即可。

比如：
1
2
3
4
5
6
28
/ \
/ \
16 30
\ / \
22 29 42
删除最小值 16 的话，将其子节点 22 把它替换掉即可（22如果有子节点保持不变）。
1
2
3
4
5
6
28
/ \
/ \
22 30
/ \
29 42

删除任意节点：

如果该节点非叶子结点、非单枝节点。需要找到该节点右子树中最接近自己值的一个节点（右子树中的最小值），这个节点自然就满足：小于所有右子树节点、大于所有左子树节点。

具体操作就是：

删除右子树最小节点并保存。
将本该被删除节点的左子树、右子树赋给刚刚保存节点的左子树右子树指针。
将本该被删除节点的父节点的指针（左或者右）指向刚刚保存的节点。
被删除节点的左子树、右子树赋为空。

复杂度分析

首先明确几个概念：

满二叉树：除了叶子结点之外，其他的节点都拥有左右子树。

满二叉树每层的节点数为：2^h （h为层数，从0层开始）

满二叉树h层的总节点数为：2^(h+1) - 1

由此就可以推出节点数 n 和层数 h 的关系：h = log 2 ^ (n+1) -1 去掉常数： O(log2 ^ n) = O(log n)

二分搜索树查询、添加、删除复杂度都是 O(log n)

完全二叉树：如果按层次为满二叉树进行编号的话，能与满二叉树编号保持一致的树称为完全二叉树。也可以说，完全二叉树比着满二叉树缺失的部分集中在整棵树的右下侧。

二叉堆

最大堆：是一个完全二叉树，堆中子节点的值总是不大于其父节点的值（只关心自己的左右子树，不包含层次之类的关系）。（同理可定义最小堆）

AVL 平衡二叉树

定义：对于任意一个叶子结点，左子树和右子树的高度的差不能超过1。

区别：

满二叉树：除了叶子结点外，所有的节点都有左右子树。
完全二叉树：按层遍历时，结果是有序（升序或降序）的。叶子结点间高度差不超过1。空缺部分一般在右下角。
线段树：是一个平衡二叉树，但不是一个完全二叉树。

平衡因子：左子树高度减去右子树高度。如果存在平衡因子大于1，表示这颗树不是平衡二叉树。

LL：如果左子树高度大于右子树超过1，使用右旋转。

// 对节点y进行向右旋转操作，返回旋转后新的根节点x
//        y                              x
//       / \                           /   \
//      x   T4     向右旋转 (y)        z     y
//     / \       - - - - - - - ->    / \   / \
//    z   T3                       T1  T2 T3 T4
//   / \
// T1   T2

RR：如果右子树高度大于左子树超过1，使用左旋转。

// 对节点y进行向左旋转操作，返回旋转后新的根节点x
//    y                             x
//  /  \                          /   \
// T1   x      向左旋转 (y)       y     z
//     / \   - - - - - - - ->   / \   / \
//   T2  z                     T1 T2 T3 T4
//      / \
//     T3 T4

对于 LR 的情况，先对左子树进行一次左旋转，变为 LL 的情况。对于 RL 的情况，先对右子树进行一次右旋转，变为 RR 的情况。

红黑树

定义：

每个节点是红色或者黑色。
根节点是黑色的。
每一个叶子结点（最后的空节点）是黑色的。
如果一个节点是红色的，那么他的孩子节点都是黑色的。
从任意一个节点到叶子结点，经过的黑色节点是一样的。
所有的红色节点都是左倾斜的。

2-3 树和红黑树具有等价性：

满足二分搜索树的接本性质，节点可以存放一个元素或者三个元素。

2-3 树是一颗绝对平衡的树。绝对平衡树：对于任意一个节点，它的左右节点一定是平衡的（高度相等）。添加时，不会添加到一个空的节点。

红黑树特性：

红黑树是保持“黑平衡”的二叉树
最大的高度 2logn O(logn)

哈希表

哈希函数的设计方法：取模，对素数取模。

设计原则：

一致性
高效性
均匀性