深度学习基础

2020-04-02

说来惭愧，好多次我参与机器学习相关的内容，做了一些产出，但最后觉得对自己来讲收获都不大。数据预处理、特征工程、机器学习算法的应用，但总觉得只是远观而没有“亵玩”，原因在于内部太多很麻烦的数学公式（高等数学、线性代数和概率在我考完试就全还回去了），唯独这次我想绕开公式从工程的角度来理解。

人工智能、机器学习与深度学习

Artificial Intelligence > Machine Learning > Deep Learning

机器学习

在预先定义好的可能性空间中，利用反馈信号的指引来寻找输入数据的有用表示。

机器学习三要素：

输入数据
预期输出数据
衡量算法效果的方法（损失函数）

所有机器学习算法都包括自动寻找这样一种变换：这种变换可以根据任务将数据转化为更加有用的表示。这些操作可能是坐标变换，也可能是线性投影(可能会破坏信息)、平移、非线性操作(比如“选择所有x>0的点”)，等等。机器学习算法在寻找这些变换时通常没有什么创造性，而仅仅是遍历一组预先定义好的操作，这组操作叫作**假设空间(hypothesis space)**。

深度学习

深度学习是机器学习的一个分支领域:它是从数据中学习表示的一种新方法，强调从连续的**层(layer)**中进行学习，这些层对应于越来越有意义的表示。

数据模型中包含多少层，这被称为模型的深度(depth)。这一领域的其他名称包括分层表示学习(layered representations learning)**和层级表示学习(hierarchical representations learning)。现代深度学习通常包含数十个甚至上百个连续的表示层，这些表示层全都是从训练数据中自动学习的。与此相反，其他机器学习方法的重点往往是仅仅学习一两层的数据表示，因此有时也被称为浅层学习(shallow learning)**。

在深度学习中，这些分层表示几乎总是通过叫作神经网络(neural network)的模型来学习得到的。可以将深度网络看作多级信息蒸馏操作:信息穿过连续的过滤器，其纯度越来越高(即对任务的帮助越来越大)。

神经网络中每层对输入数据所做的具体操作保存在该层的权重(weight)**中，其本质是一串数字。用术语来说，每层实现的变换由其权重来参数化(parameterize)。权重有时也被称为该层的参数(parameter)**。学习的意思是为神经网络的所有层找到一组权重值，使得该网络能够将每个示例输入与其目标正确地一一对应。

想要控制神经网络的输出，就需要能够衡量该输出与预期值之间的距离。这是神经网络损失函数(loss function)**的任务，该函数也叫目标函数(objective function)**。损失函数的输入是网络预测值与真实目标值(即你希望网络输出的结果)，然后计算一个距离值，衡量该网络在这个示例上的效果好坏。

深度学习的基本技巧是利用这个距离值作为反馈信号来对权重值进行微调，以降低当前示例对应的损失值。这种调节由优化器(optimizer)**来完成，它实现了所谓的反向传播(backpropagation)算法**，这是深度学习的核心算法。

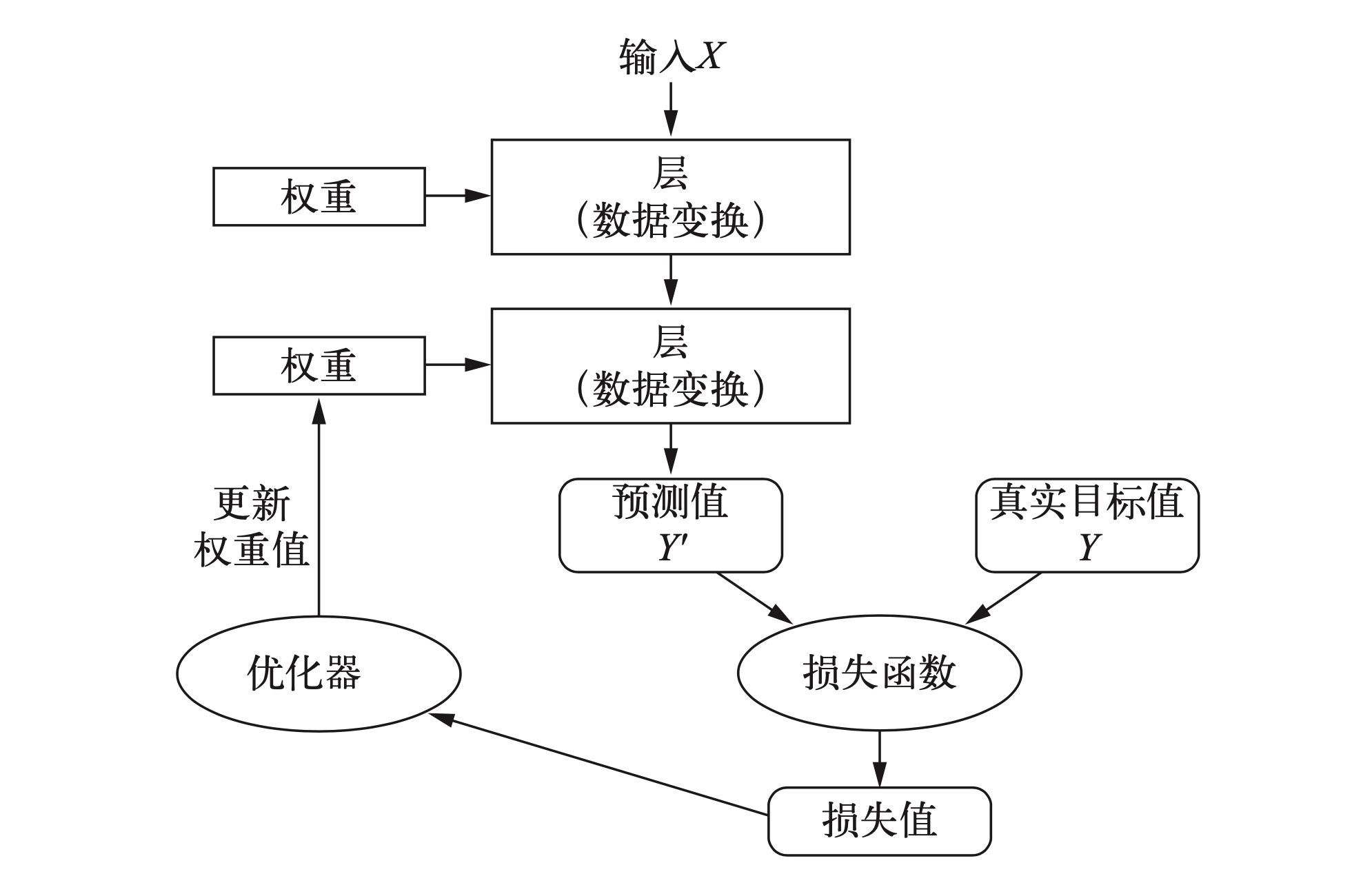
但随着网络处理的示例越来越多，权重值也在向正确的方向逐步微调，损失值也逐渐降低。这就是**训练循环(training loop)**，将这种循环重复足够多的次数(通常对数千个示例进行数十次迭代)，得到的权重值可以使损失函数最小。具有最小损失的网络，其输出值与目标值尽可能地接近，这就是训练好的网络。

深度学习简史

概率建模(probabilistic modeling)

概率建模是统计学原理在数据分析中的应用。

典型算法：

朴素贝叶斯算法，朴素贝叶斯是一类基于应用贝叶斯定理的机器学习分类器。
logistic 回归(logistic regression，简称 logreg)：虽然叫回归，但是是分类算法。

核方法(kernel method)

核方法是一组分类算法。

典型算法：

支持向量机(SVM， support vector machine)
决策边界(decision boundary)

决策树(decision tree)、随机森林(random forest)与梯度提升机(gradient bootstring machine)

决策树类似于流程图的结构，可以对输入数据点进行分类或根据给定输入来预测输出值。
随机森林首先构建许多决策树，然后将它们的输出集成在一起。随机森林适用于各种各样的问题—— 对于任何浅层的机器学习任务来说，它几乎总是第二好的算法。
梯度提升机也是将弱预测模型(通常是决策树)集成的机器学习技术。它使用了梯度提升方法，通过迭代地训练新模型来专门解决之前模型的弱点，从而改进任何机器学习模型的效果。将梯度提升技术应用于决策树时，得到的模型与随机森林具有相似的性质，但在绝大多数情况下效果都比随机森林要好。

深度学习有何不同

机器学习必须让初始输入数据更适合用这些方法处理，也必须手动为数据设计好的表示层，这叫作特征工程。与此相反，深度学习完全将这个步骤自动化:利用深度学习，你可以一次性学习所有特征，而无须自己手动设计。

三层模型中最优的第一表示层并不是单层或双层模型中最优的第一表示层。深度学习的变革性在于，模型可以在同一时间共同学习所有表示层，而不是依次连续学习(这被称为贪婪学习)。

深度学习从数据中进行学习时有两个基本特征：

通过渐进的、逐层的方式形成越来越复杂的表示;
对中间这些渐进的表示共同进行学习，每一层的变化都需要同时考虑上下两层的需要。

深度学习用于计算机视觉的两个关键思想，即卷积神经网络和反向传播。

神经网络的基础

在机器学习中，分类问题中的某个类别叫作类(class)**。数据点叫作样本(sample)。某个样本对应的类叫作标签(label)**。

数据分为：训练集(training set)**和测试集(test set)**。

神经网络的核心组件是**层(layer)**，它是一种数据处理模块，你可以将它看成数据过滤器。

层从输入数据中提取表示，大多数深度学习都是将简单的层链接起来，从而实现渐进式的**数据蒸馏(data distillation)**。

要想训练网络，我们还需要选择编译(compile)步骤的三个参数。

损失函数(loss function):网络如何衡量在训练数据上的性能，即网络如何朝着正确的方向前进。
优化器(optimizer):基于训练数据和损失函数来更新网络的机制。
**在训练和测试过程中需要监控的指标(metric)**：如正确数据所占比例。

神经网络的数据表示

数据容器如numpy中的多维数据，叫做张量(tensor)**。张量的维度(dimension)通常叫做轴(axis)**。不同维度数据有不同的术语。

0D张量叫做标量(scalar)
1D张量叫做向量(vector),例如 [1,2,3,4,5] 叫做5D向量，与5D张量不同。不过5D张量通常叫做5阶张量。
2D张量叫做矩阵(matrix)**，分为第一个轴上的数据：行(row)和第二个轴上的数据：列(column)**。
更高的一般叫做 nD 张量。

关键属性

轴的个数(阶)
形状：例如，矩阵的形状为 (3, 5)，3D 张量示例的形状为 (3, 3, 5)。向量的形状只包含一个元素，比如 (5,)，而标量的形状为空，即 ()。
数据类型：在Python中有float32、uint8、float64。

Numpy 操作张量

train_images[10:100, :, :] 可以按照不同的轴做切片。

深度学习中所有数据张量的第一个轴(0 轴，因为索引从 0 开始)都是**样本轴 (samples axis，有时也叫样本维度)**。

batch = train_images[:128]这就称作一个批量轴(batch axis)**或批量维度(batch dimension)**。因为有了批量轴时间序列数据才变成了 3D ，图像变成了 4D。

常见的数据张量

向量数据: 2D 张量，形状为 (samples, features)。如：人口统计数据集，其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值的向量，而整个数据集包含 100 000 个人，因此可以存储在形状为(100000, 3) 的 2D张量中。
时间序列数据或序列数据: 3D 张量，形状为 (samples, timesteps, features)。根据惯例，时间轴始终是第 2 个轴(索引为 1 的轴)。如：股票价格数据集。当前分钟、前一分钟、后一分钟组成一个向量，每天就有390个向量，形状为(390, 3)，250天的数据就成了(250, 390, 3)的形状。
图像: 4D 张量，形状为 (samples, height, width, channels) 或 (samples, channels, height, width)。图像通常有三个维度：高度、宽度和颜色深度。虽然灰度图像(比如 MNIST 数字图像)只有一个颜色通道，因此可以保存在 2D 张量中，但按照惯例，图像张量始终都是 3D 张量，灰度图像的彩色通道只有一维。如果图像大小为256*256，那么128张灰度图像可以保存在一个形状为(128, 256, 256, 1)的张量中，128张彩色图像可以保存在一个形状为(128, 256, 256, 3)的张量中。图像张量的形状有两种约定:**通道在后(channels-last)**的约定(在 TensorFlow 中使用)和通道在前(channels-first)的约定(在 Theano 中使用)。
视频: 5D 张量，形状为 (samples, frames, height, width, channels) 或 (samples, frames, channels, height, width)。

张量运算(tensor operation)

逐元素(element-wise)运算

即该运算独立地应用于张量中的每个元素，也就是说，这些运算非常适合大规模并行实现。

在 Numpy 中自动可以实现诸运算，如 z = x + y, z = np.maximum(z, 0.)

广播(broadcast)

如果两个大小不同的张量相加（逐运算），较小的张量会被广播，以匹配较大张量的形状。以下两个步骤：

向较小的张量添加轴(叫作广播轴)，使其ndim与较大的张量相同。
将较小的张量沿着新轴重复，使其形状与较大的张量相同。

张量点积/张量积(tensor product)

不要与逐元素乘积弄混。如 (x, y) * (y, x)的形式会得到一个标量，说白了就是线性代数中的行列式相乘。

1 2	(a, b, c, d) . (d,) -> (a, b, c) (a, b, c, d) . (d, e) -> (a, b, c, e)

张量变形(tensor reshaping)

张量变形是指改变张量的行和列，以得到想要的形状。变形后的张量的元素总个数与初始张量相同。

import numpy as np

a = np.array([[0, 1],
              [2, 3],
              [4, 5], ])

print(a.shape)
# (3, 2)

a = a.reshape(6, 1)
# [[0]
#  [1]
#  [2]
#  [3]
#  [4]
#  [5]]

print(a.shape)
# (6, 1)

# np.transpose 转置

基于梯度的优化

如 output = relu(dot(W, input) + b) 这个表达式中 W 和 b 都是张量为该层的属性，它们被称为该层的权重(weight)**或可训练参数(trainable parameter)**，分别对应kernel和bias属性。这些权重包含网络从观察训练数据中学到的信息。

一开始，这些权重矩阵取较小的随机值，这一步叫作**随机初始化(random initialization)**。当然，W 和 b 都是随机的，relu(dot(W, input) + b) 肯定不会得到任何有用的表示。虽然得到的表示是没有意义的，但这是一个起点。下一步则是根据反馈信号逐渐调节这些权重。这个逐渐调节的过程叫作训练，也就是机器学习中的学习。

上述过程发生在一个**训练循环(training loop)**内，其具体过程如下。必要时一直重复这些步骤。

抽取训练样本x和对应目标y组成的数据批量。
在 x 上运行网络[这一步叫作前向传播(forward pass)]，得到预测值 y_pred。
计算网络在这批数据上的损失，用于衡量y_pred和y之间的距离。
更新网络的所有权重，使网络在这批数据上的损失略微下降。

难点在于第四步:更新网络的权重。考虑网络中某个权重系数，你怎么知道这个系数应该增大还是减小，以及变化多少? 一种简单的解决方案是，保持网络中其他权重不变，只考虑某个标量系数，让其尝试不同的取值。假设这个系数的初始值为 0.3。对一批数据做完前向传播后，网络在这批数据上的损失是 0.5。如果你将这个系数的值改为 0.35 并重新运行前向传播，损失会增大到 0.6。但如果你将这个系数减小到 0.25，损失会减小到 0.4。在这个例子中，将这个系数减小 0.05 似乎有助于使损失最小化。对于网络中的所有系数都要重复这一过程。这种方法是非常低效的，因为对每个系数(系数很多，通常有上千个，有时甚至多达上百万个)都需要计算两次前向传播(计算代价很大)。

一种更好的方法是利用网络中所有运算都是可微(differentiable)**（也称为可导）的这一事实，计算损失相对于网络系数的梯度(gradient)**，然后向梯度的反方向改变系数，从而使损失降低。

梯度(gradient)

梯度是张量运算的导数。它是导数这一概念向多元函数导数的推广。多元函数是以张量作为输入的函数。

随机梯度下降

基于当前在随机数据批量上的损失，一点一点地对参数进行调节。由于处理的是一个可微函数，你可以计算出它的梯度，从而有效地实现第四步。沿着梯度的反方向更新权重，损失每次都会变小一点。

抽取训练样本x和对应目标y组成的数据批量。
在x上运行网络，得到预测值y_pred。
计算网络在这批数据上的损失，用于衡量y_pred和y之间的距离。
计算损失相对于网络参数的梯度[一次反向传播(backward pass)]。
将参数沿着梯度的反方向移动一点，比如 W -= step * gradient，从而使这批数据上的损失减小一点。

上面描述的方法叫作**小批量随机梯度下降(mini-batch stochastic gradient descent，SGD)**。术语随机(stochastic)是指每批数据都是随机抽取的。

注意，小批量 SGD 算法的一个变体是每次迭代时只抽取一个样本和目标，而不是抽取一批数据。这叫作真 SGD(有别于小批量 SGD)。还有另一种极端，每一次迭代都在所有数据上运行，这叫作批量 SGD。这样做的话，每次更新都更加准确，但计算代价也高得多。这两个极端之间的有效折中则是选择合理的批量大小。

SGD 还有多种变体，其区别在于计算下一次权重更新时还要考虑上一次权重更新，而不是仅仅考虑当前梯度值，比如带动量的 SGD、Adagrad、RMSProp 等变体。这些变体被称为优化方法(optimization method)**或优化器(optimizer)**。其中动量的概念尤其值得关注，它在许多变体中都有应用。动量解决了 SGD 的两个问题:收敛速度和局部极小点。

**局部极小点(local minimum)**：如果使用小学习率的 SGD 进行优化，那么优化过程可能会陷入局部极小点，导致无法找到全局最小点。

使用动量方法可以避免这样的问题，这一方法的灵感来源于物理学。有一种有用的思维图像，就是将优化过程想象成一个小球从损失函数曲线上滚下来。如果小球的动量足够大，那么它不会卡在峡谷里，最终会到达全局最小点。

链式求导: 反向传播算法

根据微积分的知识，这种函数链可以利用下面这个恒等式进行求导，它称为链式法则(chain rule): (f(g(x)))' = f'(g(x)) * g'(x)。将链式法则应用于神经网络梯度值的计算，得到的算法叫作**反向传播(backpropagation，有时也叫反式微分，reverse-mode differentiation)**。反向传播从最终损失值开始，从最顶层反向作用至最底层，利用链式法则计算每个参数对损失值的贡献大小。